Wat is de wortel van -1? Die bestaat niet, leerde je op de middelbare school. Maar wat, als je de uitkomst, het simpelste van de imaginaire getallen, i noemt? En daar verder mee gaat rekenen? Dan blijken deze imaginaire getallen wel degelijk te bestaan. En opmerkelijk magisch en nuttig te zijn… (video)
Draaiing door imaginaire getallen
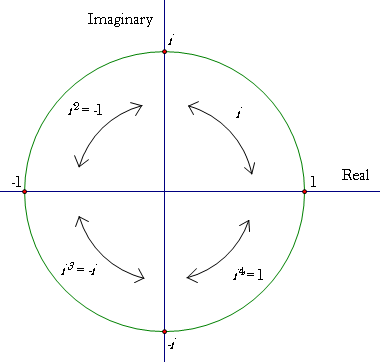
Een voorbeeld. Als we reële getallen op de x-as en imaginaire getallen op de y-as plotten, kunnen we complexe getallen weergeven. Een complex getal is een getal dat uit zowel een reëel deel als uit een imaginair deel bestaat. Dus het imaginaire getal 2i zou dan twee eenheden boven de oorsprong liggen. Door met i te vermenigvuldigen, beginnen getallen op dit oppervlak rond de nul te draaien, steeds met negentig graden. De 2i wordt in dit voorbeeld nu -2 en draait negentig graden tegen de klok in.
Ruimte, tijd, magnetisme en imaginaire getallen
Tijd is volgens de speciale relativiteitstheorie, houd je vast, een imaginaire ruimtedimensie. In een euclidische ruimte had er alleen elektrische lading bestaan. Geen magnetisme. Magnetisme is imaginaire elektrische lading. Magnetisme bestaat alleen omdat elektrische lading beweegt. Een dergelijke ruimte, met tijd als imaginaire dimensie, kan worden beschreven met behulp van een Minkovski metriek.
Visionair.nl kan overigens geen aansprakelijkheid aanvaarden voor lezers die zich beroepen op de imaginaire aard van de tijdsdimensie. Bijvoorbeeld om deurwaarders of boze bazen af te wimpelen. Of voor lezers die letsel oplopen door een supermagneet. Imaginair is hier meer dan echt.
Bombelli en Hero van Alexandrië
De uitvinder van i was de Italiaanse wiskundige Rafael Bombelli, die een eerder idee van Hero van Alexandrië omtrent deze getallen uitwerkte. Hero is meer bekend van de allereerste stoommachine, maar legde dus ook de basis voor deze revolutie in de wiskunde. Weinig mensen stonden er toen bij stil dat hij hiermee de wiskundige beschrijving van kwantummechanica, de relativiteitstheorie, elektromagnetisme en zelfs fractals mogelijk maakte. Kortom: geen moderne wereld zoals wij die nu kennen zonder deze “getallen die niet bestaan”….
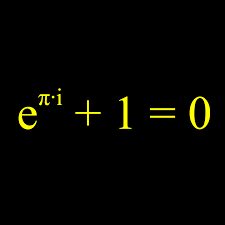
Het bericht Imaginaire getallen opmerkelijk nuttig in echte wereld verscheen eerst op Visionair.